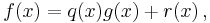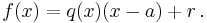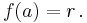Polynomial remainder theorem
In algebra, the polynomial remainder theorem or little Bézout's theorem[1] is an application of polynomial long division. It states that the remainder of a polynomial 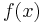 divided by a linear divisor
divided by a linear divisor 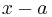 is equal to
is equal to 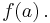
Contents |
Example
Let 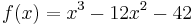 . Polynomial division of
. Polynomial division of 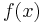 by
by 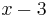 gives the quotient
gives the quotient 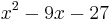 and the remainder
and the remainder 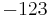 . Therefore,
. Therefore, 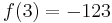 .
.
Proof
The polynomial remainder theorem follows from the definition of polynomial long division; denoting the divisor, quotient and remainder by, respectively, 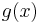 ,
, 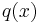 , and
, and 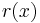 , polynomial long division gives a solution of the equation
, polynomial long division gives a solution of the equation
where the degree of 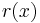 is less than that of
is less than that of 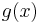 .
.
If we take 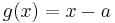 as the divisor, giving the degree of
as the divisor, giving the degree of 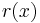 as 0, i.e.
as 0, i.e. 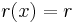 :
:
Setting  we obtain:
we obtain:
Applications
The polynomial remainder theorem may be used to evaluate 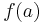 by calculating the remainder,
by calculating the remainder,  . Although polynomial long division is more difficult than evaluating the function itself, synthetic division is computationally easier. Thus, the function may be more "cheaply" evaluated using synthetic division and the polynomial remainder theorem.
. Although polynomial long division is more difficult than evaluating the function itself, synthetic division is computationally easier. Thus, the function may be more "cheaply" evaluated using synthetic division and the polynomial remainder theorem.
The factor theorem is another application of the remainder theorem: if the remainder is zero, then the linear divisor is a factor. Repeated application of the factor theorem may be used to factorize the polynomial.
References
- ^ Piotr Rudnicki (2004). "Little Bézout Theorem (Factor Theorem)". Formalized Mathematics 12 (1): 49–58. http://mizar.org/fm/2004-12/pdf12-1/uproots.pdf.